# 前言
数学作为学习和研究现代科学技术必不可少的基本工具，在各个行业都发挥着重要的作用。在前端中，包括但不仅限于canvas动画，数学知识都是必不可少的。以画布左上角顶点为原点建立的坐标系中，平移，旋转，变换这些都跟数学息息相关，这里就总结下前端中会用到的数学知识。
# 基本概念
把长度等于半径长的弧所对的圆心角叫做1弧度的角，用符号rad表示，读作弧度。
如果半径为r的圆心角α所对弧的长为l,那么角α的弧度数的绝对值是
弧度和角度转换公式：
# 三角函数
三角函数在这里我们不涉及太多的公式，只回顾一些基础的知识。
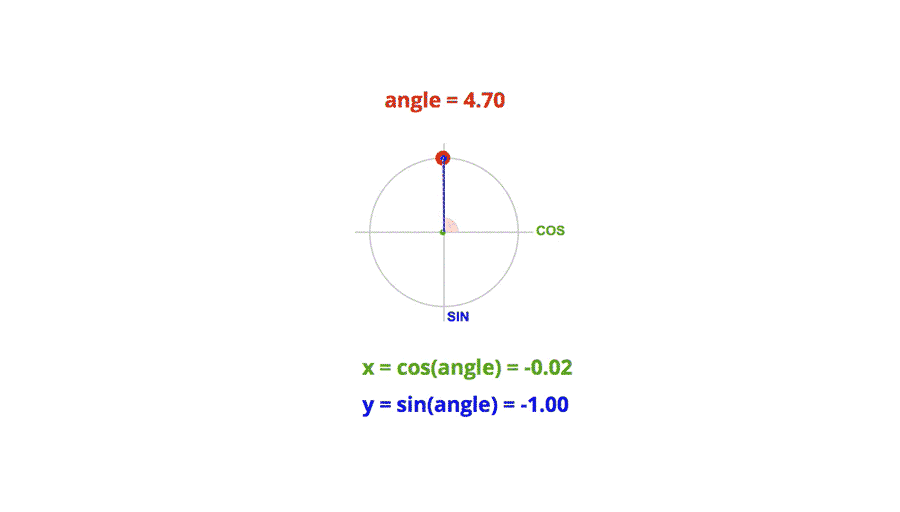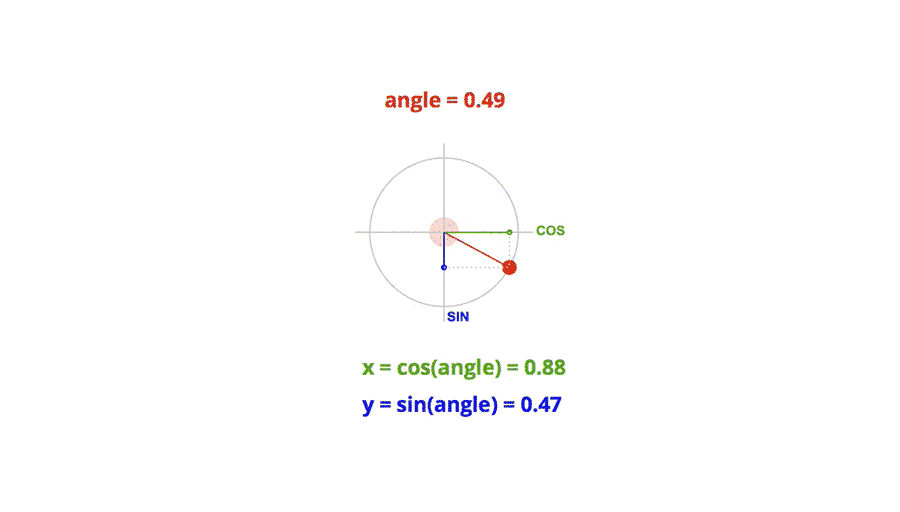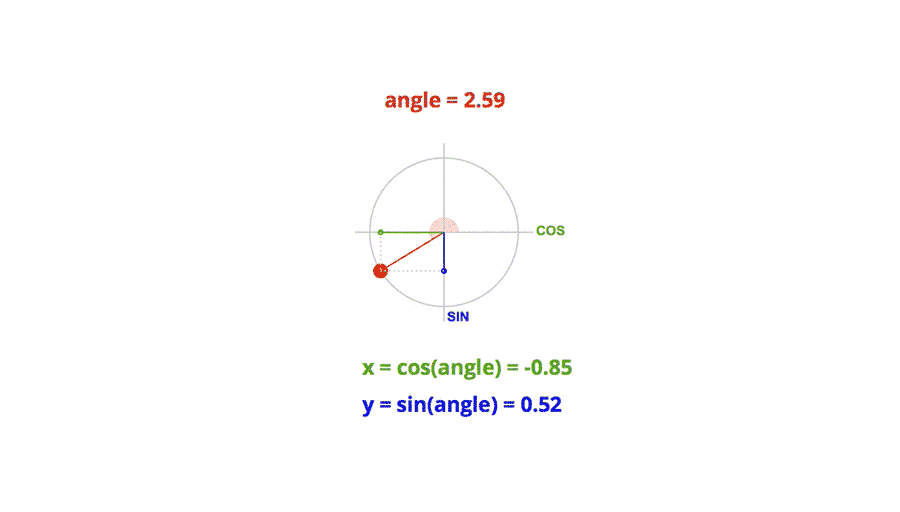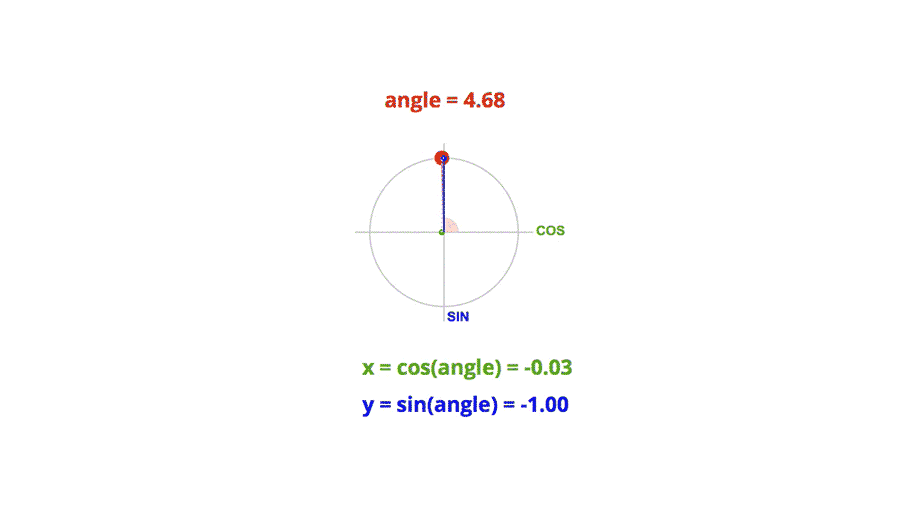
在笛卡尔直角坐标系中，半径为单位长度的圆上任意一点的横坐标就是对应角度的余弦值，任意一点的纵坐标就是对应角度的正弦值。
图片来源于三角函数在前端动画中的应用, 侵删
# 简单的图像变换
以正弦曲线为例，对函数进行简单的变换，可以得到不一样的结果。图片来源于三角函数在前端动画中的应用，侵删
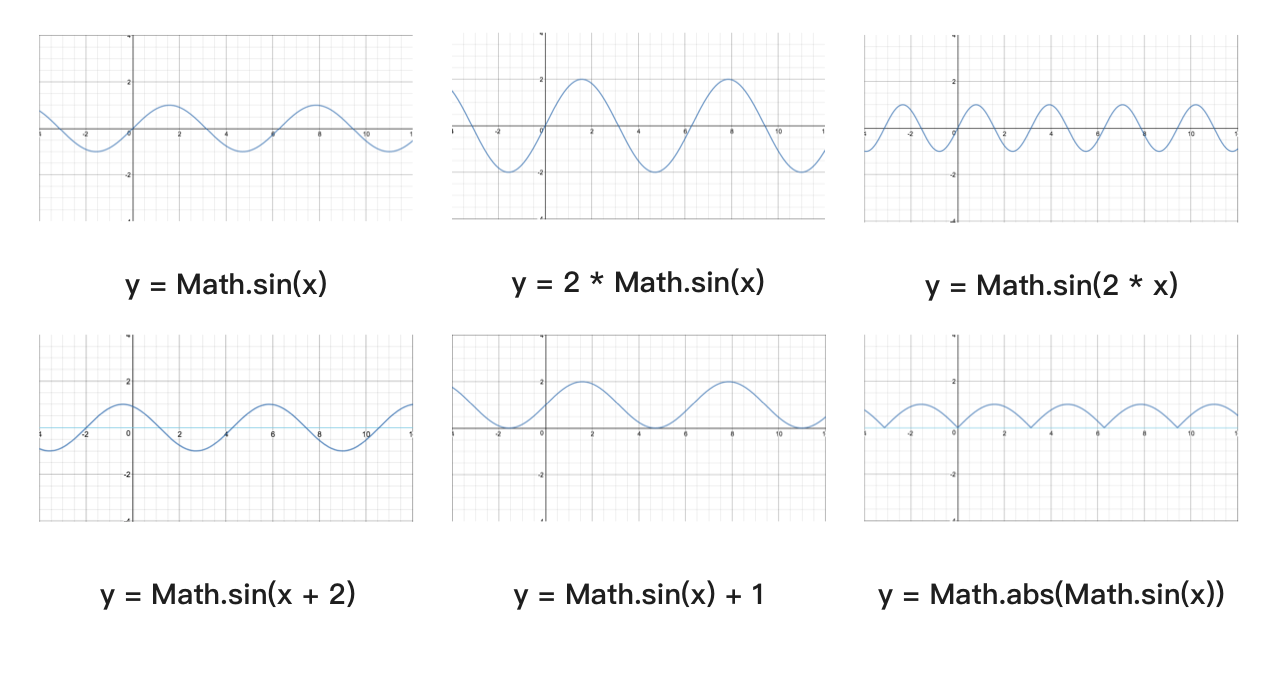
正弦曲线公式：y = A sin(Bx + C) + D
- A 控制振幅，A 值越大，波峰和波谷越大，A 值越小，波峰和波谷越小；
- B 值会影响周期，B 值越大，那么周期越短，B 值越小，周期越长。
- C 值会影响图像左右移动，C 值为正数，图像左移，C 值为负数，图像右移。
- D 值控制上下移动。
说起三角公式，有两个比较有意思的东西需要说一说。
# 奇变偶不变，符号看象限
对于kπ/2±α(k∈Z)的三角函数值， ①当k是偶数时，得到α的同名函数值，即函数名不改变； ②当k是奇数时，得到α相应的余函数值，即sin→cos;cos→sin;tan→cot,cot→tan. （奇变偶不变） 然后在前面加上把α看成锐角时原函数值的符号。（符号看象限） 第一象限内任何一个角的三角函数值都是“+”； 第二象限内只有正弦、余割是“+”，其余全部是“－”； 第三象限内只有正切、余切函数是“+”，弦函数是“－”； 第四象限内只有余弦、正割是“+”，其余全部是“－”。
# 两角和差的正选余弦公式
假设我们将这么一张长方形的纸进行对折，折到一个角刚好靠到一个边上。
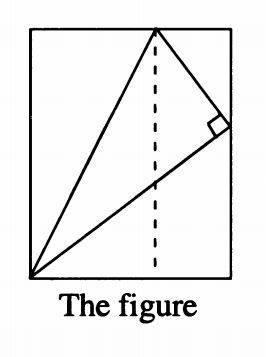
然后我们设被折的那个角是β，剩下的那个角是α，马上得到一对相似三角形，一对全等三角形。同时我们知道被折掉的那个三角形的两边分别是sinβ和cosβ。
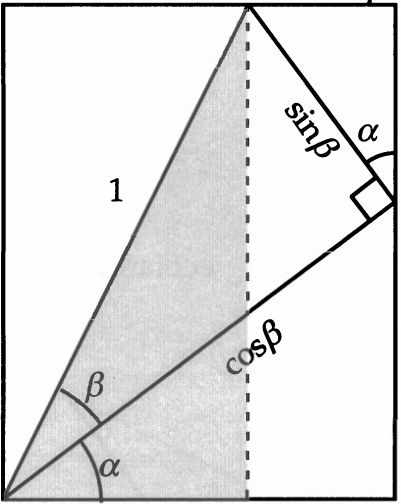
我们让 sinβ 和 cosβ 继续向两边投影。得到 sinαsinβ、 cosαsinβ、 sinαcosβ、 cosαcosβ
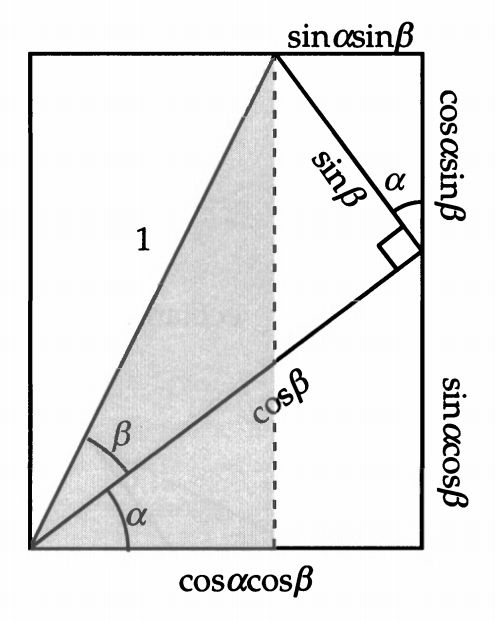
我们可以发现一个规律，就是“贴在墙上的”，也就是纵向的都是sin与cos交错，这很好理解。因为最右边的一对相似三角形的方向是不一样的，由此而得到的投影也是不一样的。而横向的总是cos成对出现或sin成对出现。这当然是因为两次投影方向相同。好的，铺陈工作到此完毕。现在我们可以开始推导出公式了。让我们把目光聚焦到左下角的一个大角 。显然，它的余弦值等于阴影部分在底边的长度，而它的正弦值就等于大长方形的侧边长度。于是得到：
如果我们保持两个角α和β不变，而仅仅把大长方形的底边设为1，那么得
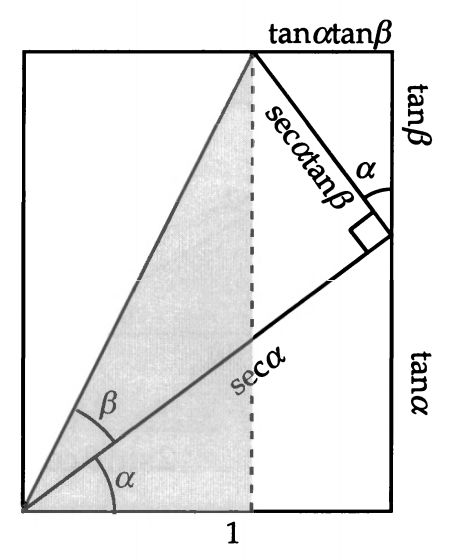
显然，被我们对折的那个三角形的长边现在变成了 secα ，其短边变为 secαtanβ。它们继续投影，分别得到tanα、 1、 tanβ、 tanαtanβ。这时候
另一方面，让我们再次尝试对这张长方形的纸进行折叠。这次仍然假设被折叠的那个角叫做β，然后把两倍的β称作α。
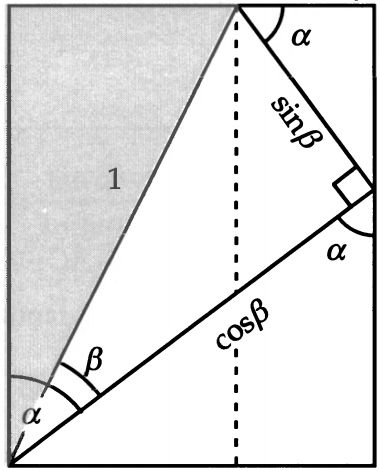
被折叠的三角形的长边和短边仍然是 cosβ 和 sinβ 。继续投影分别得到：
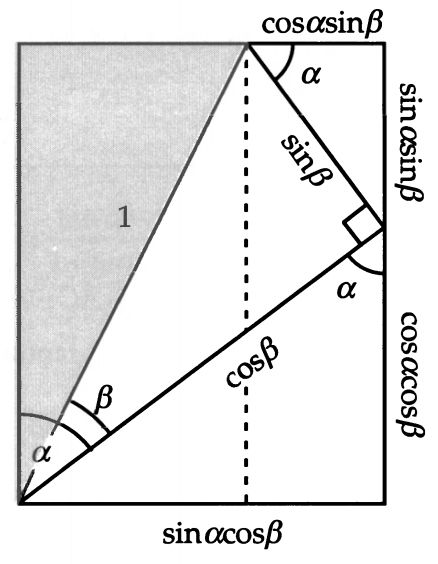
这回，凡是纵向的都是成对的cos或sin，而横向的都是cos与sin交错了。对于 (α-β) 这个角（其实也就是β），我们有：
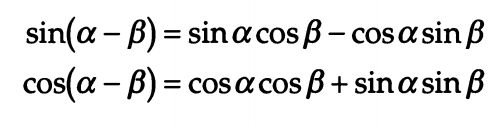
如果保留α和β两个角，仅仅将一条边定为1，则底边变为 tan α
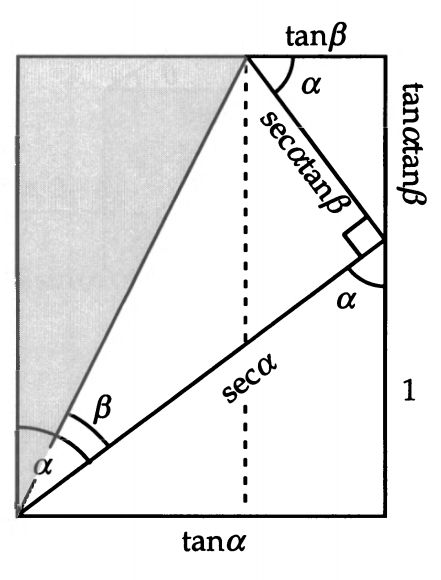
于是：
至此，我们用一张图推出了六个恒等式。
# 圆的方程
# 椭圆的标准方程
# 双曲线的标准方程
# 抛物线的标准方程
参考资料： [1] 三角函数在前端动画中的应用 [2] 高中数学学那么多三角函数公式到底有什么用？